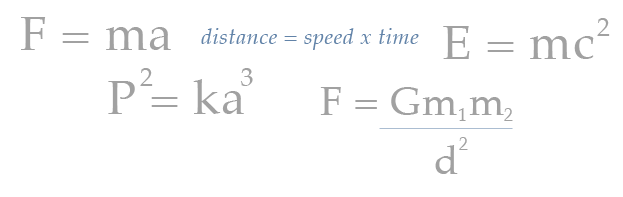Voyage’s Use of Numerical Models

A Numerical Model uses mathematical equations to represent some reality to be studied. It is the familiarity with mathematics—the language of nature—that allows the student to embrace the equations, test the equations against observable real world variables, and make predictions.

This plot is from the teacher’s answer key for the Voyage grade 5-8 lesson Round and Round We Go – Exploring Orbits in the Solar System. The lesson looks at dynamics in the Solar System, and includes two inquiry-based hands-on activities. The first activity explores the nature of an ellipse based on its mathematical properties. Objectives include: an understanding of the mathematical parameters that define and characterize an ellipse; developing the ability to precisely draw an ellipse; understanding how the shape—the eccentricity—of the ellipse changes with a change in the distance between the foci; and an understanding that objects orbiting the Sun travel in ellipses of varying size, eccentricity, and spatial orientation. In the second activity the class explores how they might create a good model of the orbits in the Solar System. This plot is that model, and is created by the students from the real orbital parameters of the Solar System that are provided to them.

Orbits in the Solar System (click on the image for more detail)

In Voyage’s case, the central numerical model is the equation of scale:

Model Dimension = Real Dimension/10,000,000,000

It is used heavily in the educational materials, allowing students to calculate, on the scale of Voyage, the sizes of the Sun, planets, moons, and other Solar System objects, as well as the speed of a planet orbiting the Sun, the speed and location of spacecraft such as Voyager 1 and 2, and the speed of light. The equation of scale is used by students to create a physical model of the Solar System, and to characterize how such a model would be set in motion.

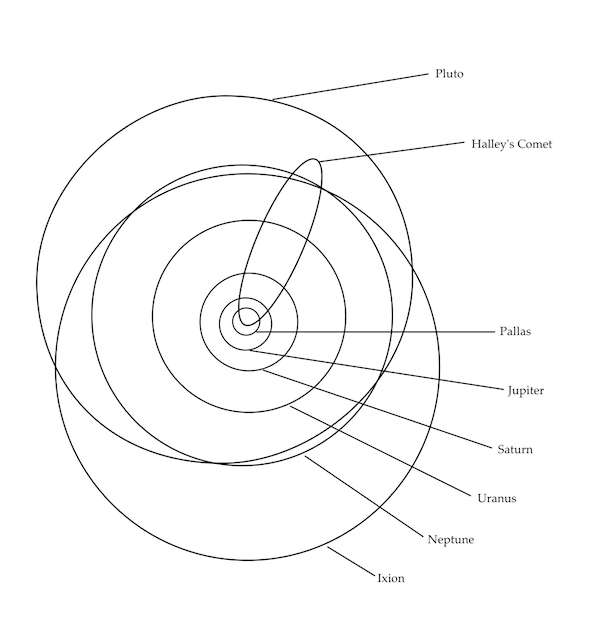
Another example of a numerical model used in Voyage is a middle school lesson that uses the equation of an ellipse, coupled with known parameters defining the planetary orbits, to create a physical model of orbits in the Solar System (see the diagram to the right). The student then explores the nature of the generated ellipses and sees that the planets orbit the Sun in nearly circular orbits. But the orbits for a comet and a Trans-Neptunian Object have far more elliptical orbits than the planets. This is also the case for Pluto, which provides some evidence that Pluto might be a large Trans-Neptunian Object rather than a small planet.

At the high school level, the apparent size of the Sun in photographs taken at different times of the year is used to generate the equation of Earth’s orbit around the Sun, and a physical model of that orbit.

Navigation